Demos#
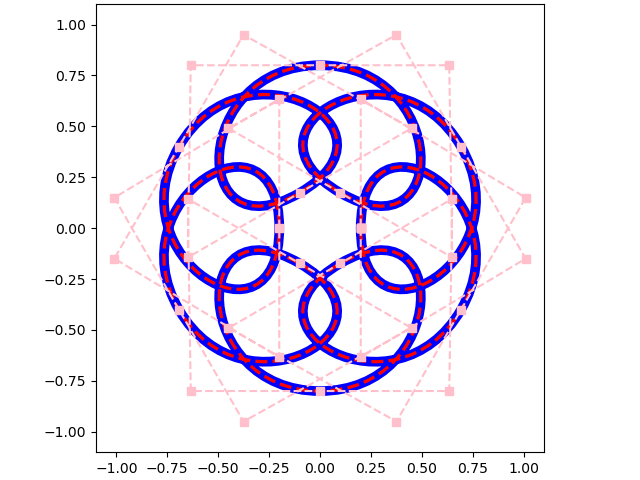
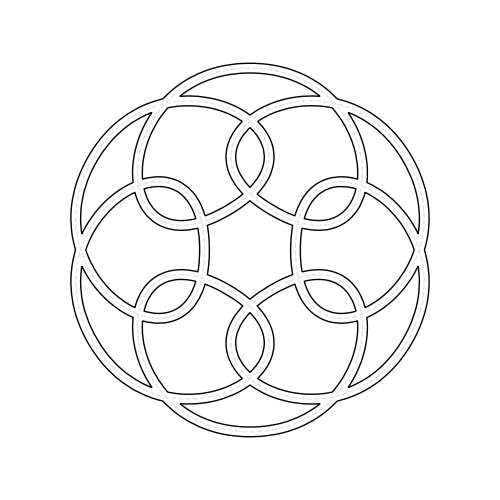
Reflection Knots#
These are curves made by reflecting a “unit cell” to generate the complete knot
def knot1():
return path_from_pts(
[
(Pt(0, 0.8), np.rad2deg(np.pi)),
(Pt(-0.7, 0.15), np.rad2deg(-np.pi / 10)),
(Pt(-0.7, 0.7), 0),
(Pt(0.5, -0.75), np.rad2deg(-np.pi / 2)),
(Pt(-0.8, 0), np.rad2deg(-np.pi / 2)),
],
)
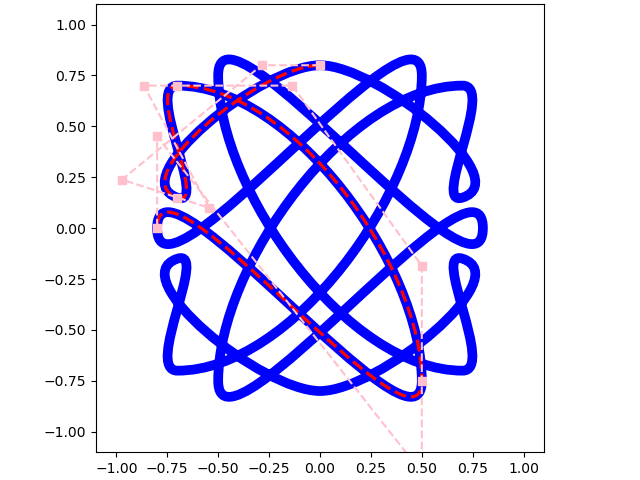
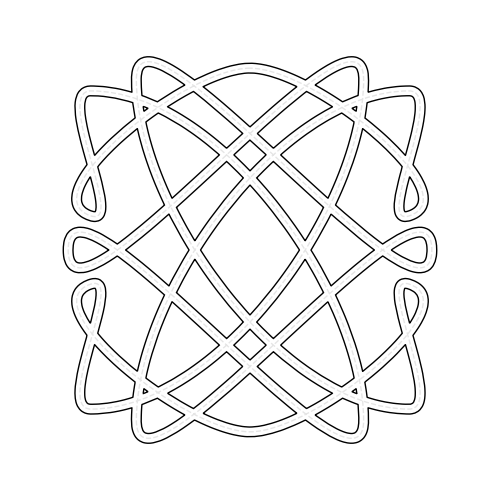
Bands#
Running linear bands inspired by page boarders. In principle these should be tiled from one unit, but are currently just fixed length (and bigger than the view)
def band1():
return path_from_pts(
[
(Pt(x, y), 0)
for (x, y) in zip(
np.arange(-2, 2, 0.1),
cycle([-0.55, 0.55]),
)
],
scale=0.7,
closed=False,
)
(Source code, png, svg, pdf)
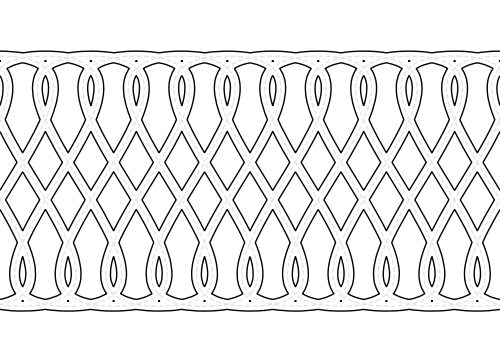
def band2():
return path_from_pts(
[
(Pt(x, y), np.rad2deg(angle))
for (x, y, angle) in zip(
np.arange(-2, 2, 0.2),
cycle([-0.55, 0.55]),
cycle([0, np.pi]),
)
],
scale=0.7,
closed=False,
)
(Source code, png, svg, pdf)
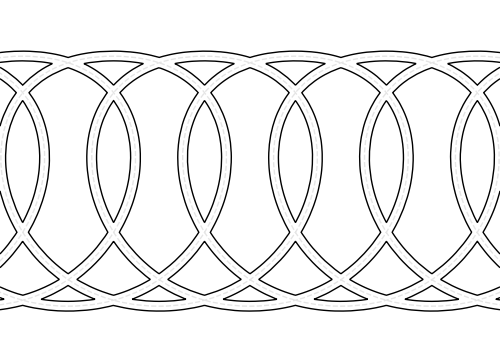
Rings#
def ring1():
r = 0.5
return path_from_pts(
[
(
Pt(np.cos(th) * (r + dr), np.sin(th) * (r - dr)),
np.rad2deg(th - np.pi / 2),
)
for (th, dr) in zip(np.linspace(0, 2 * np.pi, 13), cycle([-0.4, 0.4]))
],
scale=1,
closed=True,
)
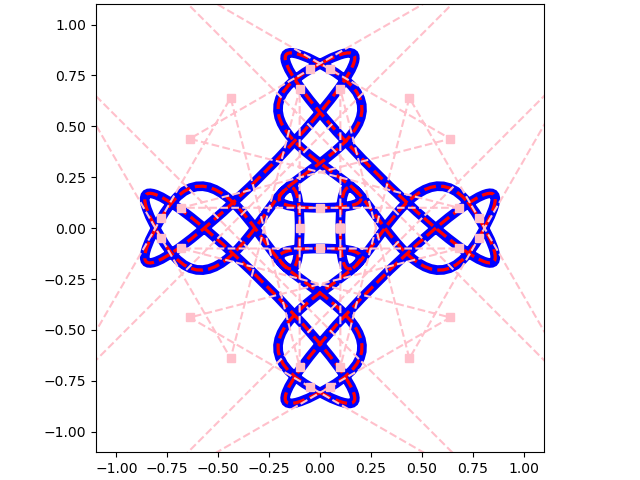

def ring2():
r = 0.5
return path_from_pts(
[
(
Pt(np.cos(th) * (r + dr), np.sin(th) * (r + dr)),
np.rad2deg(th + phi),
)
for (th, dr, phi) in zip(
np.linspace(0, 2 * np.pi, 13),
cycle([-0.3, 0.3]),
cycle([-np.pi / 2, np.pi / 2]),
)
],
scale=1,
closed=True,
)